Decode Every Angle: Types of Triangles and Their Defining Properties

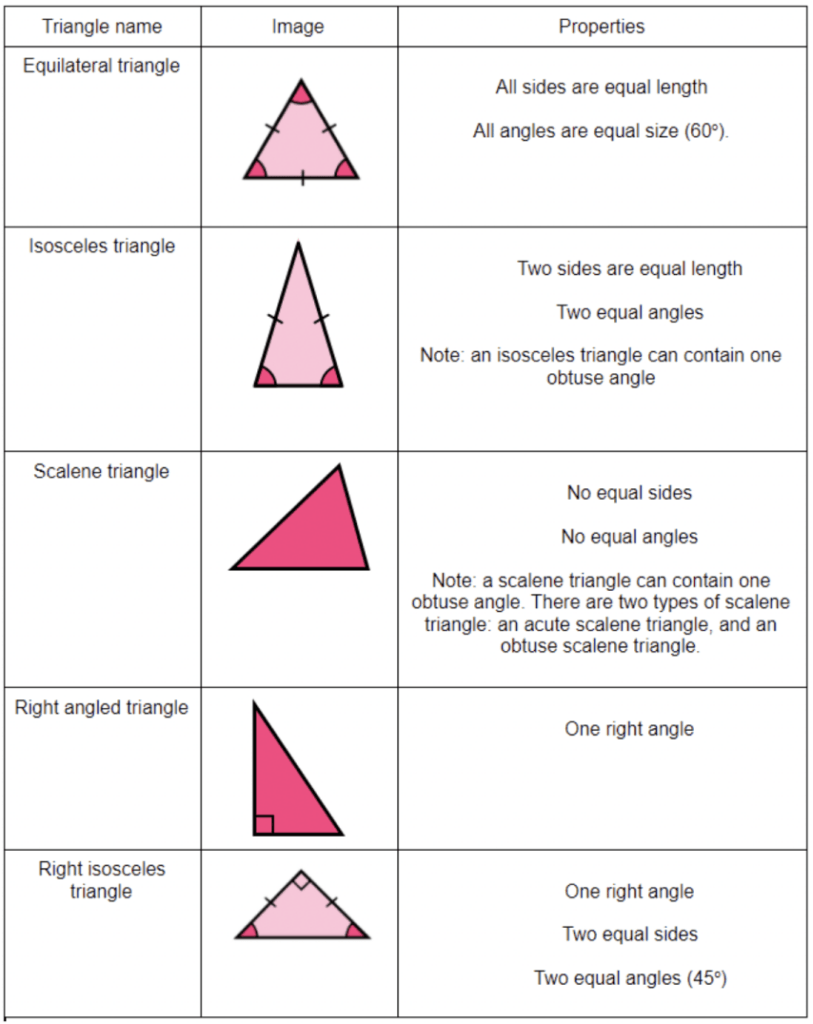
Triangles—geometric wonders that form the backbone of architectural design, engineering precision, and mathematical reasoning. From towering skyscrapers anchored by isosceles stability to the sharply pointed spires of Gothic cathedrals, their structure relies on three distinct forms governed by precise angle relationships and properties. Understanding the types of triangles—scalene, isosceles, and equilateral—not only unlocks insights into geometry but also reveals how these shapes influence real-world applications.

Each triangle class, defined by side lengths and interior angles, embodies unique mathematical behavior, making them essential to both theoretical study and practical problem-solving in fields ranging from trigonometry to construction.

Scalene Triangles: No Equal Angles, No Equal Battles

The scalene triangle stands out as the most varied of the three types, defined by three unequal sides and, as a consequence, three unequal angles. “Each angle tells a different story,” notes renowned geometrist Dr.

Elena Torres, “because no two sides—or angles—are alike.” This lack of symmetry means no sides or angles are easily predictable, requiring full measurement and calculation. With no repeated elements, scalene triangles exhibit a dynamic range of angle sums: always adding to 180 degrees, but varying widely within that constraint. Examples include the classic 60-70-50 degree configuration or the more extreme 30-65-85 degree setup.

Because no symmetry reduces redundancy, scalene triangles challenge users to rely on the sine and cosine laws for angle and side determination. Their flexibility makes them indispensable in surveying, where irregular land boundaries demand precise, individual triangle analysis. In mechanical design, scalene configurations often model corrective joints and non-repetitive load paths, offering versatility unmatched by more constrained forms.

Beyond versatility, scalene triangles highlight geometry’s complexity: each triangle is a unique geometric entity requiring full contextual analysis rather than assumptions based on symmetry. This individuality demands careful measurement and often advanced trigonometric tools to unlock their full potential.

Isosceles Triangles: Balance Meets Efficiency

Defined by two equal sides and, by extension, two equal angles opposite those sides, the isosceles triangle strikes a balance between structure and simplicity. This inherent symmetry reduces complexity, enabling faster calculations and clear geometric stability—qualities valued in both education and engineering.

The defining property of isosceles triangles is the Angle-Side-Side Converse: angles opposite equal sides are congruent. If the base angles measure 45 degrees each, the vertex angle must be 90 degrees, yielding a perfectly symmetrical triangle ideal for balance-driven applications. This characteristic also ensures the triangle’s altitude from the vertex bisects the base and creates two congruent right triangles, simplifying area and perimeter computations.

In structural engineering, isosceles shapes feature in bridge trusses and roof supports, where symmetry evenly distributes stress. Architecturally, these triangles appear in balanced façades and decorative elements that demand visual harmony without unnecessary complexity. Their predictable geometry allows designers to optimize material use while preserving aesthetic integrity.

The isosceles triangle’s blend of symmetry and flexibility makes it a workhorse of geometric design—where balance meets functionality, ensuring both visual appeal and structural reliability.

Equilateral Triangles: Perfect Symmetry in Every Corner

The equilateral triangle is geometry’s pinnacle of balance: three equal sides, three equal angles, and rotational symmetry that makes it identical from every angle. Each interior angle measures exactly 60 degrees, forming a shape that epitomizes perfection and uniformity. Often described as the most aesthetically pleasing figure, it transcends mere mathematics to become a universal symbol of harmony.

Foundational in geometry education, equilateral triangles are the first non-trivial case studied beyond basic right or isosceles forms. Their internal symmetry supports multiple angle theorems—for example, the centrality of the 60-degree angle in proofs involving centroids, incenters, and circumcenters. This symmetry also enables seamless tessellation, allowing infinite repetition without gaps, a property frequently exploited in tilework, packaging design, and digital graphics.

Beyond visual appeal, equilateral triangles excel in efficiency. In nature, honeycombs purposefully form hexagons derived from six equilateral triangles, maximizing space while minimizing construction effort. In engineering, their symmetry supports pressure-distribution principles seen in geodesic domes and symmetric load-bearing structures.

As both a mathematical truth and a design ideal, the equilateral triangle proves that symmetry is not just beautiful—it’s functionally optimal.

While simpler in appearance, the equilateral triangle’s universal symmetry and mathematical elegance make it a cornerstone of design and problem-solving, embodying perfection in both theory and practical application.

The Mathematical Foundation: Angle Sums and Trigonometric Laws

Across all triangle types, the sum of interior angles remains a constant: always 180 degrees. This foundational truth governs not only basic geometry but also advanced trigonometry.

Yet, while scalene triangles demand full angle resolution through sine and cosine laws, isosceles and equilateral configurations permit quicker determinations using symmetry. In equilateral triangles, the central 60-degree angle enables easy identification of centroids and medians, which coincide at the same point—a feature absent in