Mastering Trigonometry Across the Quadrants: How Angles Define the Plane

Quadrants and trigonometric functions are not just abstract concepts confined to textbooks—they form the backbone of navigation, engineering, physics, and even digital graphics. Understanding how sine, cosine, and tangent behave across each of the four quadrants reveals powerful patterns that underpin countless real-world applications. From calculating satellite trajectories to analyzing waveforms, the nuanced interplay of angle signs and function values empowers precise analysis in both theoretical and applied mathematics.

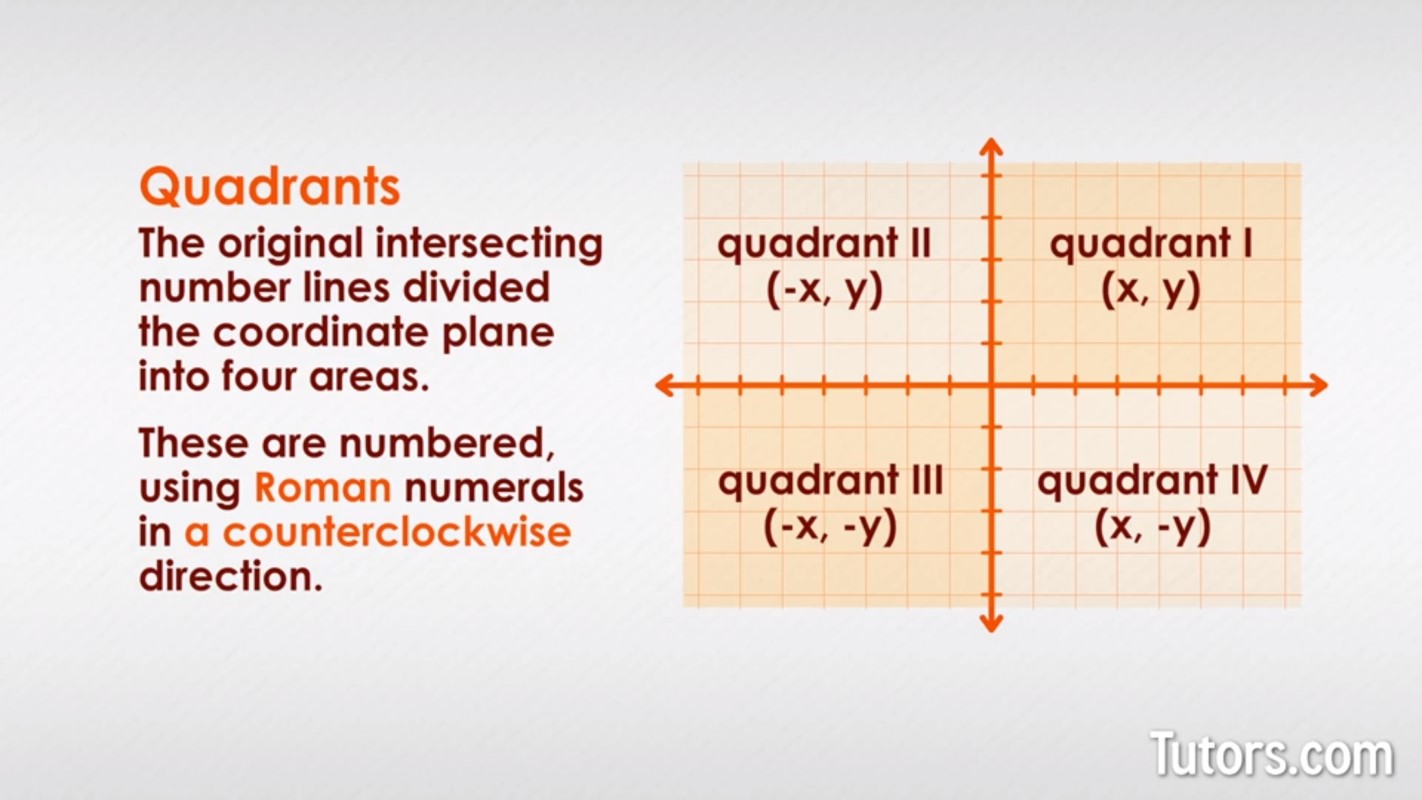
Trigonometry fundamentally deals with angles and their relationships to triangles and the unit circle. Each angle measured from the positive x-axis is assigned to one of four quadrants—Q1 (0° to 90°), Q2 (90° to 180°), Q3 (180° to 270°), and Q4 (270° to 360°)—and these divisions govern how trigonometric functions behave. This quadrant-based approach enables consistent evaluation, regardless of an angle’s size, making trigonometry a universal language for spatial reasoning.

The Role of Angle Sign in Trigonometric Sign Patterns

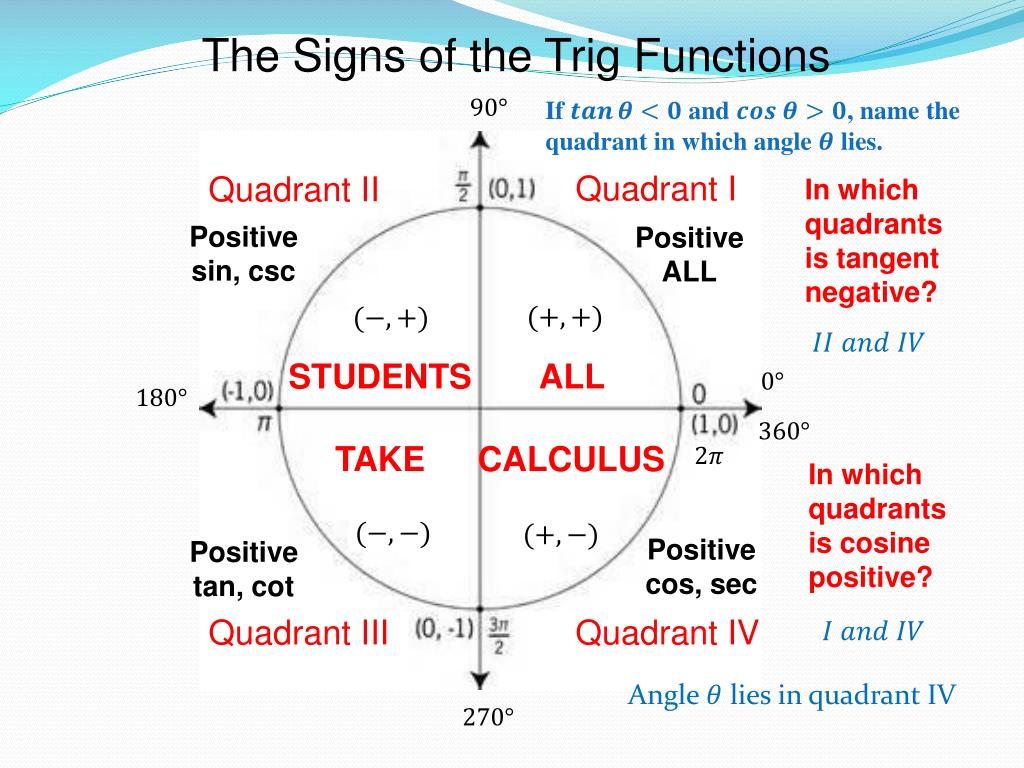
The sign of sine, cosine, and tangent depends critically on quadrant placement, captured succinctly by mnemonic “All Students Take Calculus” — a rule that maps function signs to each quadrant: - In

Q1: All functions positive

, sine, cosine, and tangent are positive.

- In

Q2: Sine positive, cosine and tangent negative

, only sine retains its positivity. - In

Q3: Tangent positive, sine and cosine negative

, cosine and tangent dominate in sign. - In

Q4: Cosine positive, sine and tangent negative

, cosine is the only positive value.

This pattern reveals a disciplined structure beneath apparent complexity: “A student takes calculus” serves as a memorable guide to trig function behavior, transforming abstract rules into intuitive memory aids. Understanding this order is essential for accurate computation, especially when evaluating expressions involving multiple angles or transforming coordinates across quadrants.

The unit circle diagram illuminates these sign changes clearly: starting at Q1 where both x and y are positive, moving counterclockwise triggers sign shifts.

At 90°, sine peaks positive, cosine collapses to zero; 180° flips cosine to negative; 270° flips sine negative; 360° resets to Q1. Each 90° step alters coordinate signs in accordance with quadrant transitions, reinforcing spatial intuition.

Navigating the Coordinate Plane: Trigonometry by Quadrant

Quadrants serve as the coordinate plane’s reference framework, directly influencing both angle interpretation and trigonometric outputs. In Q1, where x and y are both positive, both cosine and sine yield positive values: - \(\cos \theta > 0\), \(\sin \theta > 0\), \(\tan \theta = \frac{\sin}{\cos} > 0\) This quadrant defines foundational scenarios—such as projectile motion launching at shallow angles—where motion components depend on both horizontal and vertical trigonometric contributions.

In Q2, the x-coordinate turns negative while y remains positive, leading to: - \(\cos \theta < 0\), \(\sin \theta > 0\), \(\tan \theta < 0\) This setup is critical in navigation, where directional vectors often require vector components rotated eastward and southward, common in aviation and maritime pathfinding. Moving to Q3, both coordinates are negative—quantities of sine and cosine become negative with positive tangent: - \(\cos \theta < 0\), \(\sin \theta < 0\), \(\tan \theta > 0\) This quadrant’s behavior is essential