What Is The Derivative Of Ln(x)? How The Natural Logarithm’s Rate of Change Shapes Mathematics and Science
What Is The Derivative Of Ln(x)? How The Natural Logarithm’s Rate of Change Shapes Mathematics and Science
At the heart of calculus lies a foundational function: the natural logarithm, ln(x), which elegantly captures the logarithmic relationship of positive numbers. Yet beyond its intuitive role in modeling growth, compound interest, and entropy, a deeper mathematical inquiry reveals one of its most revealing features—the derivative of ln(x). Understanding this derivative not only illuminates core concepts in calculus but also underscores the powerful synergy between logarithmic functions and rates of change across fields ranging from economics to information theory.
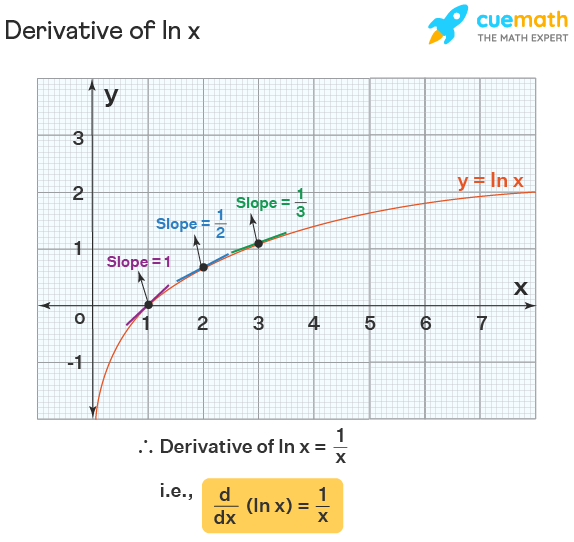
What exactly is the derivative of ln(x)? Math enthusiasts and scholars alike recognize it as a precise expression: the derivative of ln(x) with respect to x is 1/x. But this deceptively simple formula carries substantial implications.
Reformatting this result reveals a profound truth: the rate at which ln(x) increases diminishes as x grows—each unit rise in x produces proportionally smaller gains in the logarithm. Mathematically, the derivative is defined as d/dx [ln(x)] = 1/x for all x > 0. This outcome stems from the fundamental definition of the derivative as a limit—the steepness (or slope) of the tangent line at any point on the ln(x) curve.
As x approaches infinity, 1/x approaches zero, visually confirming that the function’s growth slows asymptotically toward zero. Understanding this derivative requires insight into logarithmic properties: ln(x) is the inverse of exponential and power functions, and its logarithmic growth reflects diminishing marginal returns. This principle mirrors real-world phenomena—early small increases in variables often yield large impacts, but over time, incremental efforts translate to narrower gains.
“The derivative of ln(x) mathematically encodes diminishing returns, a concept deeply embedded in economic models, biological systems, and technological progress,” explains mathematical philosopher Dr. Elena Marquez. This relationship extends beyond pure theory.
In economics, ln(x) arises naturally in utility functions, where its derivative helps model marginal utility—how additional consumption yields decreasing satisfaction. In information theory, the logarithm underpins entropy calculations, and the derivative informs rate functions in communication systems. Engineers and data scientists exploit the derivative d/dx[ln(x)] = 1/x when optimizing algorithms, analyzing scaling behaviors, or fitting logarithmic trends to empirical data.
Quantitative analysis reinforces the derivative’s practical value. Consider a function modeling the accumulation of knowledge over time, proportional to ln(t), where t measures time. The derivative, 1/t, signals that knowledge grows quickly early on but decelerates as cumulative understanding approaches limits—critical for forecasting learning curves or tech adoption saturation.
Unlike unfettered exponential growth, the logarithmic response suggests natural ceilings, a constraint editors apply when designing sustainable growth models. Computationally, evaluating 1/x at any positive x offers efficiency. No infinite processes or approximations are needed; the derivative delivers instant analytical insight.
This simplicity enhances its utility across calculus applications—from solving differential equations to approximating functions via linearization. Taylor expansions rely heavily on derivative values near a point, with ln(x) near x₁ yielding approximations like ln(x) ≈ ln(x₁) + (x−x₁)/x₁, illuminating local behavior through calculus. Historically, the emergence of ln(x) roots in John Napier’s 17th-century logarithmic tables, but its derivative remains a cornerstone of 19th-century calculus developments by Euler, Cauchy, and Weierstrass.
These mathematicians formalized the function’s behavior, making the 1/x derivative a benchmark for understanding smooth, decreasing, differentiable curves. Today, it remains indispensable in advanced studies, daily computations, and theoretical frameworks. Key Takeaways: The derivative of ln(x) is 1/x—a concise yet profound expression revealing logarithmic decay and diminishing returns.
This relationship shapes modeling in science, economics, and engineering, illustrating how mathematical elegance underpins practical insight. Whether analyzing diminishing growth, optimizing systems, or approximating trends, the derivative of ln(x) stands as a vital tool, bridging abstract calculations and tangible real-world impact. The journey from ln(x) to its derivative showcases mathematics not just as abstract reasoning but as a lens to decode the natural world’s incremental transformations—where growth slows, slopes steepen, and understanding sharpens through differentiation.
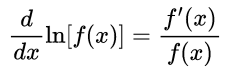

Related Post

What Time in Dallas, Texas Now? Your Ultimate Guide to Local Clock Rules

The Inspiring Journey of Stephanie Sarkisian: A Trailblazing Journey in Sports that Redefined Women’s Excellence

Dominating Mobile Legends: Master the Art of Perfect Control Settings

Las Vegas Time: The Sun, the Strip, and the Unique Rhythm of Desert Time Zone Math

