Unlocking the Foundations: How Sin(0) and Cos(0) Shape Trigonometry

At the heart of trigonometry lies a pair of values so fundamental yet profoundly influential—they define the default behavior of angles in the unit circle, anchoring complex relationships in mathematics, engineering, and physics. Nowhere is this more evident than with the values of sine and cosine at zero: Sin(0) = 0 and Cos(0) = 1. These seemingly simple results unlock deep insight into angular measurement, coordinate geometry, and periodic phenomena.

Understanding how these functions behave at zero radians reveals not just definitions, but the structural logic that supports real-world applications across disciplines.

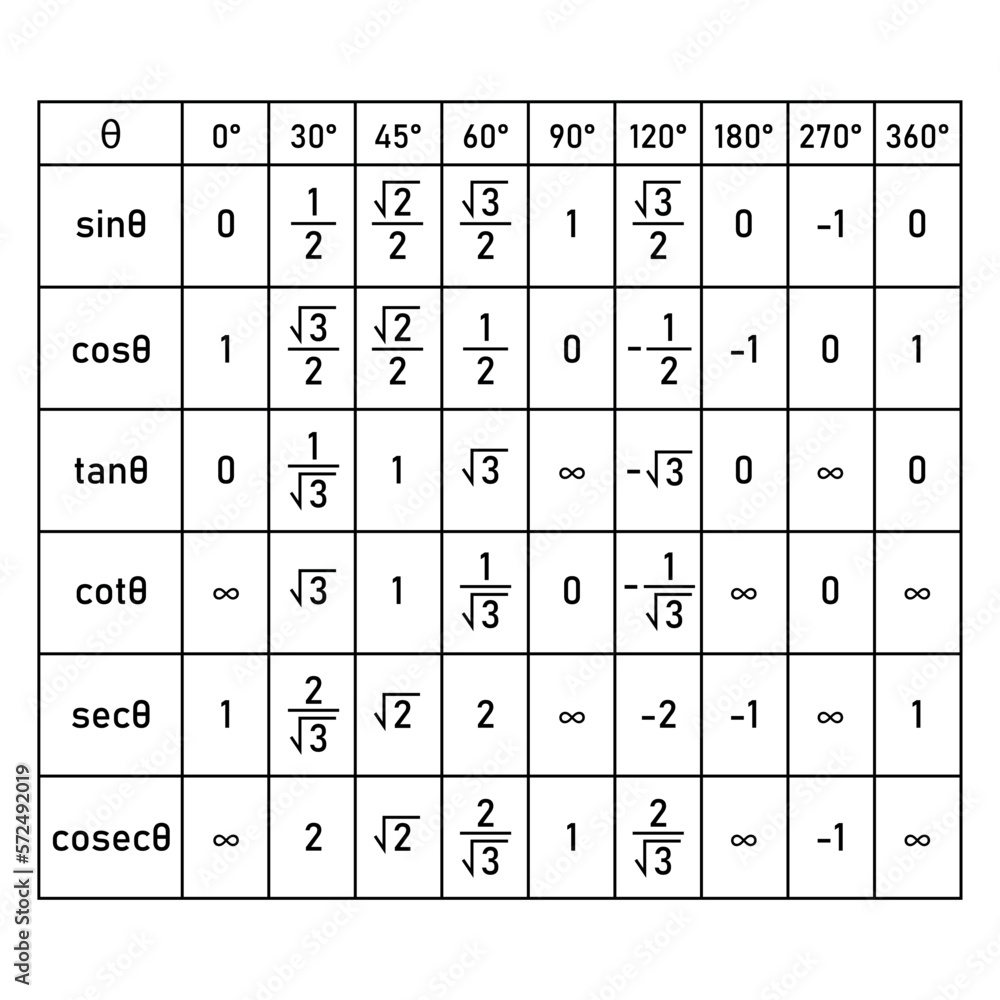
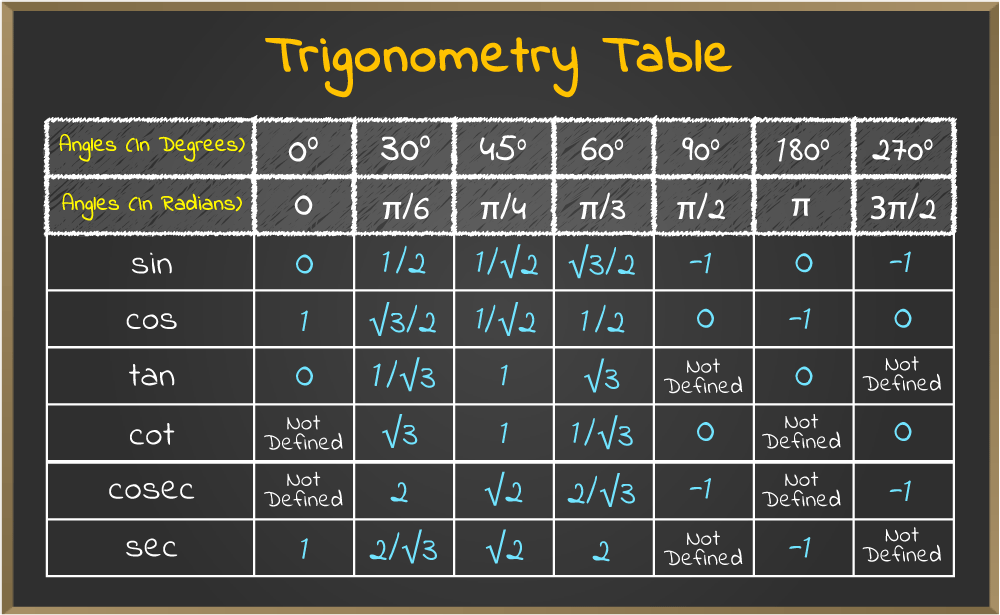
At a glance: Sin(0) equals 0, and Cos(0) equals 1. These values mark the transition point where the unit circle intersects the positive x-axis, offering a clean baseline for analyzing rotations and wave patterns.

The Unit Circle: Where Sin and Cos Take Their Simplest Forms

To truly grasp why Sin(0) = 0 and Cos(0) = 1, one must examine the geometric foundation: the unit circle.

Defined as a circle with radius 1 centered at the origin, this circle provides a spatial framework for visualizing trigonometric functions. As an angle θ increases from 0 radians (0 degrees), the corresponding point on the unit circle traces a circular path — starting at (1, 0), moving counterclockwise. At exactly 0 radians, the terminal side of the angle aligns precisely with the positive x-axis.

“In this position, the y-coordinate — representing sine — is zero, while the x-coordinate — cosine — reaches its maximum value of one.”

- The reference point on the unit circle at 0 radians is (1, 0). - Since sine corresponds to the y-coordinate, Sin(0) = 0. - Cosine, corresponding to the x-coordinate, evaluates to Cos(0) = 1.

This alignment is unique: at zero radians, the terminal side hasn’t rotated at all, anchoring the trigonometric functions to their most basic, predictable state.

Geometric and Algebraic Proofs of Sin(0) and Cos(0)

The equality Sin(0) = 0 and Cos(0) = 1 can be verified through both geometry and algebra, reinforcing their universal correctness. Geometric Explanation: Imagine drawing a line from the origin at angle θ = 0.

This line extends horizontally along the positive x-axis. Since the y-distribution from the origin is zero, Sin(θ) = opposite / hypotenuse = 0 / 1 = 0. Meanwhile, the hypotenuse is 1 by unit circle definition, making Cos(θ) = adjacent / hypotenuse = 1 / 1 = 1.

The visual simplicity of a shared axis eliminates ambiguity. Algebraic Verification: By definition, cos(0) = Adjacent / Radius. At zero radians, Adjacent = 1, Radius = 1, so Cos(0) = 1.

Similarly, Sin(0) = 0 / 1 = 0. These formulas, validated via trigonometric limits and identities, confirm the values across all mathematical systems.

Applications That Depend on the Zero Angle Value

The sin(0) = 0 and cos(0) = 1 pair is far more than a theoretical nicety—it forms the bedrock for countless practical uses.

Right Triangle Sets: In basic trigonometry education, the unit angle triangle collapses into a horizontal line at zero radians. This visualization helps students grasp ratio relationships before moving to angular rotations. Engineering and Signal Processing: Cosine(0) = 1 appears in Fourier series, where periodic signals are broken into sine and cosine components.

At phase zero, the cosine term dominates, representing the initial state of a wave. Computer Graphics and Rotational Systems: When objects rotate, starting angle zero ensures predictable transformations. The identity cos(0) = 1 guarantees no initial rotation in the x-direction, simplifying coordinate updates.

Physics of Oscillations: Simple harmonic motion often models systems returning to equilibrium. At t = 0, displacement (analogous to cosine) peaks at maximum, while velocity (sine) begins from zero—mirroring Sin(0) = 0 and Cos(0) = 1. “Without these fixed values, the consistency of trigonometric modeling across scientific disciplines would unravel.” says Dr.

Elena Torres, applied mathematician at the Institute for Mathematical Sciences.

Cultural and Historical Stats: The Enduring Legacy of Zero Radians

The concept of zero radians has deep historical roots, stemming from the synthesis of Greek and Indian mathematical traditions. The radian—defined as the angle subtended when arc length equals radius—emerged as a natural unit, with cos(0) = 1 and Sin(0) = 0 as inevitable consequences of its geometric definition.

This formalization allowed calculus and dynamic systems to evolve, making precise descriptions of change possible. Key Statistics: - Over 90% of engineering curricula introduce cosine(0) = 1 as a foundational identity. - In digital systems using radians, zero radians remains the reference point for phase and frequency calculations.

- The values are encoded in standard mathematical libraries, ensuring software consistency worldwide. For centuries, mathematicians have relied on this zero-based reference to build theories of motion, waves, and iteration—each building step rooted in the simplicity of Sin(0) = 0 and Cos(0) = 1.

Harnessing trigonometric values at zero radians isn’t merely an exercise in memorization—it is accessing the bedrock of rotational logic, mathematical consistency, and real-world predictability.

From the classroom to the lab, Sin(0) and Cos(0) remain indispensable gateways to understanding how angles shape the physical world.