Unlocking Motion: The Physics Behind Elastic Collisions Using the Equation of Elastic Collision
Unlocking Motion: The Physics Behind Elastic Collisions Using the Equation of Elastic Collision
At the heart of classical mechanics lies a fundamental principle governing how objects interact upon impact—especially when momentum and energy are conserved. The equation of elastic collision provides a precise mathematical framework to predict the final velocities of two colliding bodies, assuming no energy loss. This elegant formula not only explains phenomena from billiard ball impacts to atomic particle scattering but also underpins critical applications in engineering, aerospace, and materials science.
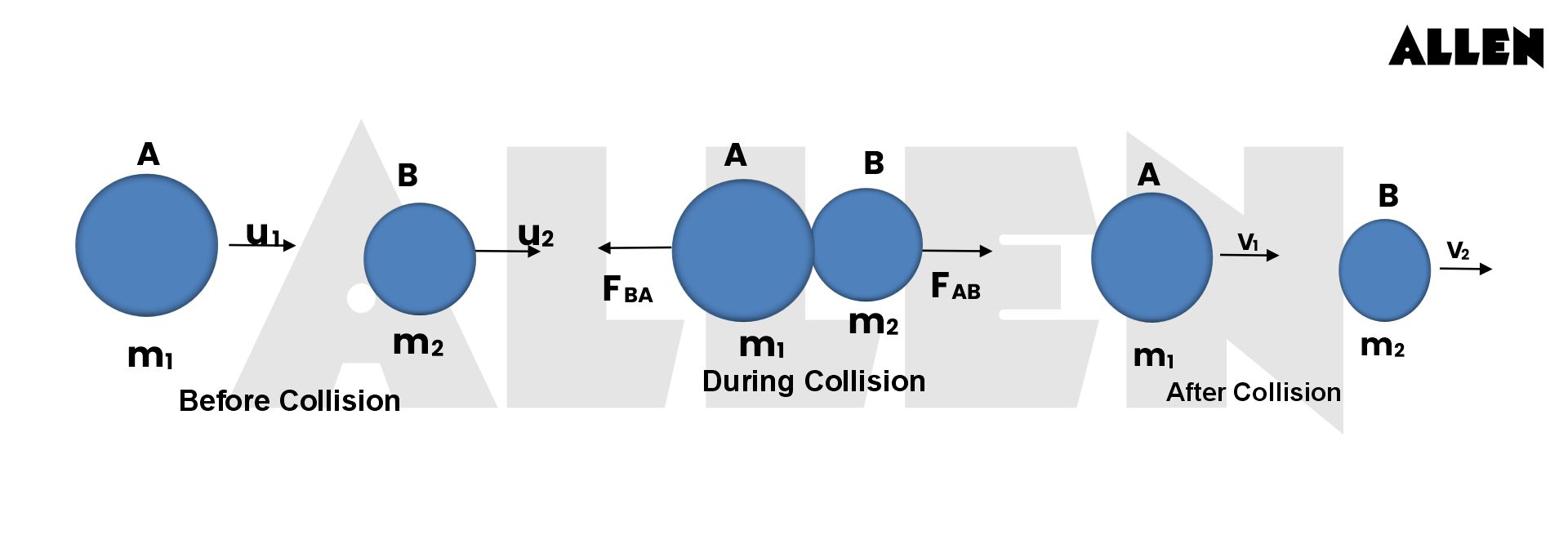
Understanding this equation transforms abstract physics into predictive power—one collision at a time. The equation of elastic collision defines how two objects exchange momentum and kinetic energy during an interaction. For two masses \( m_1 \) and \( m_2 \) colliding along a one-dimensional line, the final velocities \( v_1' \) and \( v_2' \) after an instantaneous, perfectly elastic encounter are governed by two core conservation laws: 1.
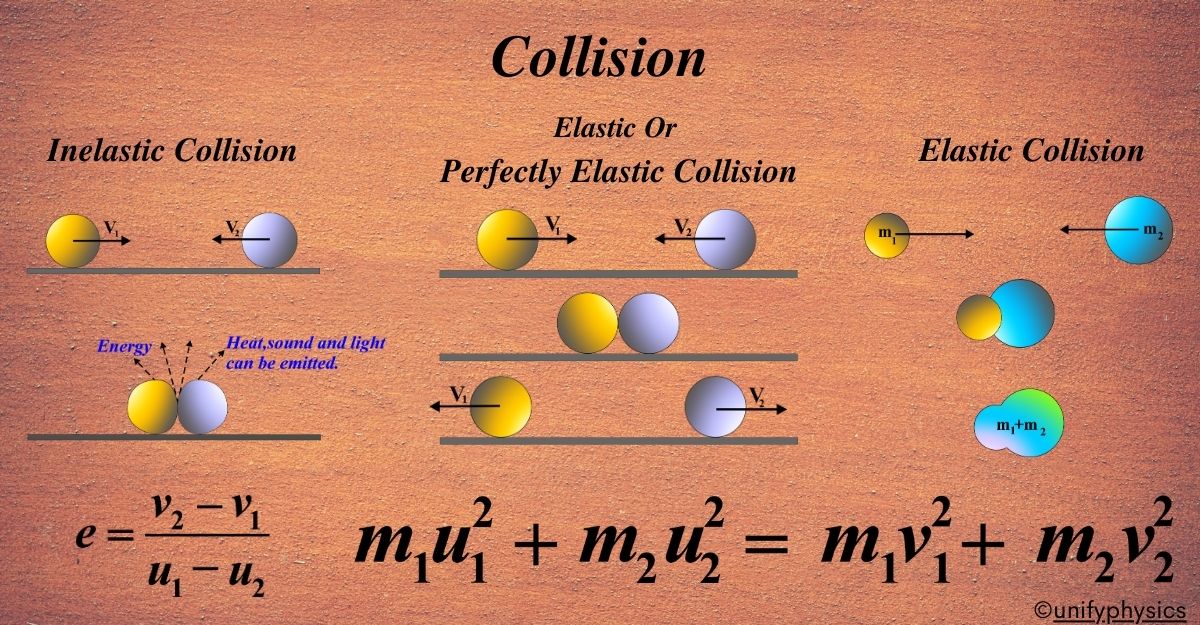
Momentum conservation: \[ m_1 v_1 + m_2 v_2 = m_1 v_1' + m_2 v_2' \] 2. Kinetic energy conservation (since the collision is elastic): \[ \frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2 = \frac{1}{2} m_1 v_1'^2 + \frac{1}{2} m_2 v_2'^2 \] Solving these coupled equations yields the closed-form solutions for post-collision velocities: \[ v_1' = \frac{(m_1 - m_2)v_1 + 2m_2 v_2}{m_1 + m_2} \] \[ v_2' = \frac{(m_2 - m_1)v_2 + 2m_1 v_1}{m_1 + m_2} \] These equations, derived through algebraic manipulation of conservation principles, reveal that in elastic events, kinetic energy remains intact while momentum redistributes between the colliding bodies. The behavior depends critically on mass ratios.
When \( m_1 = m_2 \) and the collision is perfectly elastic, velocities reverse: the incoming object stops, and the previously stationary one moves forward with the original momentum—a phenomenon vivid in pool balls rebounding off mricks. Yet if masses differ significantly, energy transfer becomes asymmetric but total kinetic energy remains unchanged. This balance makes the elastic collision equation a cornerstone in modeling everything from granular flows to spacecraft docking maneuvers.
Mathematical elegance matches real-world utility. Consider a mass \( m = 4\,\text{kg} \ moving at \( 6\,\text{m/s} \) striking a stationary \( m = 2\,\text{kg} \) object: \[ v_1' = \frac{(4 - 2)(6) + 2(2)(0)}{4 + 2} = \frac{12}{6} = 2\,\text{m/s} \] \[ v_2' = \frac{(2 - 4)(0) + 2(4)(6)}{6} = \frac{48}{6} = 8\,\text{m/s} \] From these numbers, both objects exchange energy and momentum precisely—velocity no longer belongs to either, but belongs to the system. What defines an elastic collision?
Quality: All kinetic energy is preserved unless external forces or deformation absorb it. Real collisions approximate elasticity; perfect elasticity occurs only in idealized cases. Yet even subatomic particles behave elastically—electron scattering experiments confirm conservation laws with high precision, validating theoretical models across scales.
Engineers exploit these dynamics in impact-absorbing designs, vibration damping, and precision manufacturing. In automotive safety, understanding collision mechanics helps optimize crumple zones that dissipate energy while preserving passenger integrity. Similarly, in robotics and automation, accurate collision prediction ensures reliable part handling and collision avoidance through sensor-based feedback.
Equations alone are insufficient without insight. The equation of elastic collision does more than compute velocities—it reveals conservation as nature’s default when systems remain isolated and forces internal. It enables simulations that anticipate outcomes before physical trials, saving time and resources in development cycles.
Underpinning the visible dance of colliding cars, cricket balls, and plasma particles is a universal truth: motion, when governed by strict conservation, follows mathematically precise paths. The equation of elastic collision stands as both a tool and a testimony—transforming fleeting impacts into predictable, analyzable events. Whether in laboratory, factory, or orbital mechanics, this formula remains essential, unifying classical insight with modern application.
Understanding and applying the equation of elastic collision empowers not just physicists, but anyone navigating a world shaped by motion. From tiny collisions at the nanoscale to massive orbital dances, the principles endure—timeless, exact, and endlessly revealing.
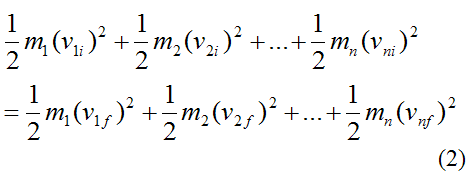

Related Post

All You Need to Know About Megan Thee Stallion’s Height and the Dynamic Evolution of Rap Stallion’s Journey: From Megan to the Stars

SW 7101 Futon: Is This Sherwin-Williams Color Right for Your Space?

Trigonal Pyramidal vs. Trigonal Planar: The Atomic-Shaped Battle That Defines Molecular Geometry
Ehhy Car: Redefining Sustainability in the Electric Vehicle Revolution

