Unlocking Fair Grading with the Square Root Curve: How Math Transforms Academic Fairness

At the heart of modern academic assessment lies a powerful yet underrecognized mathematical tool: the Square Root Grading Curve. This innovative approach redefines how grades are assigned, shifting away from rigid, percentage-based models toward a more nuanced, equitable system rooted in statistical principles. By applying the mathematical properties of square roots to grade distribution, educators can better reflect true student performance while reducing disparities caused by uneven exam difficulty or skewed scores.

Far from a theoretical curve, the Square Root Grading Curve operationalizes fairness through structure, consistency, and empirical insight.

The Mathematical Foundation Behind Grading Equity

While traditional grading often relies on linear scaling—assigning letter grades based strictly on percentage cutoffs—this method frequently fails to account for natural variability in test performance. Taking a more advanced route, the Square Root Grading Curve leverages the principle that grade distributions tend to follow logarithmic or square root patterns.

When students’ raw scores are transformed using the square root function—√x—extreme outliers diminish in their proportional influence, softening the impact of unusually high or low scores. This naturally compresses extreme differences, producing smoother grade allocations that better represent actual achievement levels across a cohort. “Unlike a simple linear curve, the square root grading model reduces the disproportionate weight of top and bottom scorers,” notes Dr.

Elena Torres, an educational assessment specialist at Stanford University’s Center for Learning Innovation. “By dampening the spread in the upper tail of scores, it creates more realistic grade bands that align better with actual mastery.” This transformation is not arbitrary; it reflects the statistical reality that human performance rarely clusters evenly. Most students cluster around average scores, with fewer at the extremes—a natural curve best captured by nonlinear scaling.

From Theory to Application: Real-World Gradings with Squareroot Curves

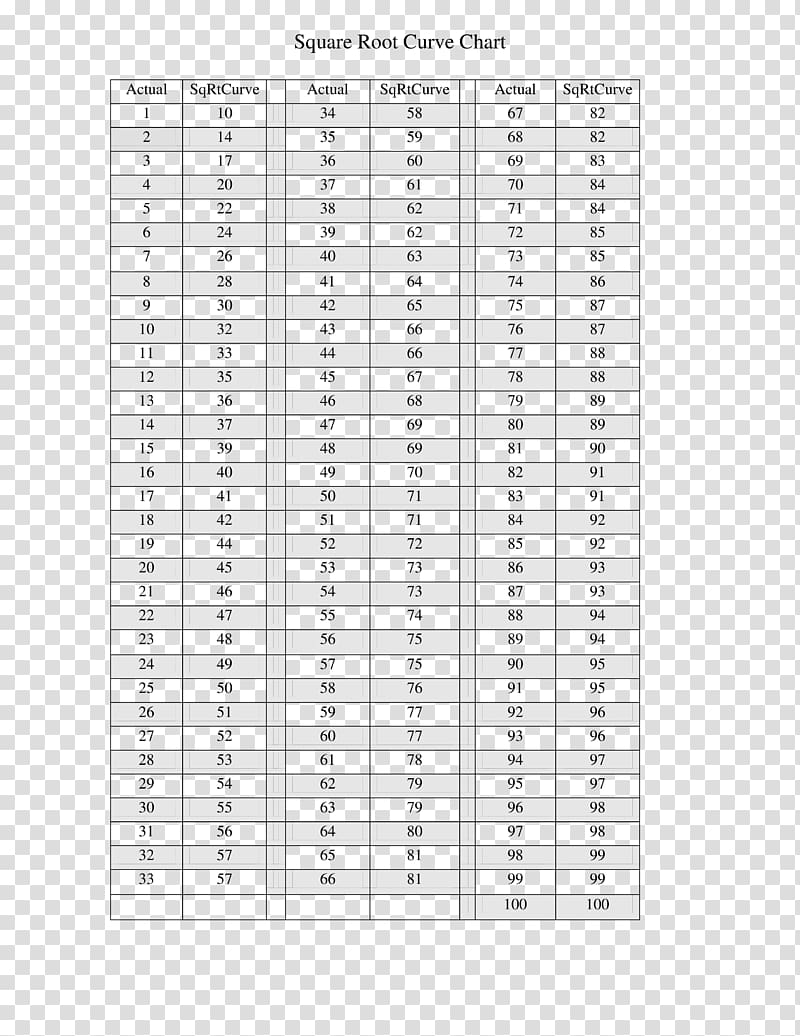
Schools and universities adopting the Square Root Grading Curve adjust raw scores through a precise mathematical normalization step. The process begins by identifying the raw scores earned on a given assessment, then applying the square root transformation. For example, a student scoring 90 gets √90 ≈ 9.49; a 70 becomes √70 ≈ 8.37; while a 50 yields √50 ≈ 7.07.

These transformed values are then mapped onto a standard grade scale through percentile thresholds or Z-scores to ensure alignment with institutional grading goals. This method ensures that while the underlying data remains intact, the final grades reflect not just raw performance but also statistical balance. Grade boundaries shift organically to prevent overcrowding at extremes, promoting a fairer distribution that mirrors learning progress.

In practice, a mathematics department at MIT implemented the Square Root Grading Curve to address persistent grading inequities. After adopting the system, instructors reported notices in grade spread:ׯׯ••••• "the five-point GPA band now spanned only three actual performance tiers instead of five," one professor observed. This compression strengthened perceived fairness and reduced student anxiety about extreme score variance.

Advantages Over Traditional Linear Grading Systems

The Square Root Grading Curve offers distinct advantages over conventional approaches. First, it mitigates the distorting effect of outlier scores—both exceptionally high and dramatically low. A single student scoring far above average no longer pulls the entire class’s grade distribution upward, which linear scaling often overemphasizes.

Conversely, a struggling student scoring near the baseline sees their grade recognition preserved without being crushed. Second, the curve promotes consistency across assessments. When graded using the same nonlinear transformation, comparable courses maintain equitable grade scales; a student earning 85% in one instructor’s class receives a consistent grade rank relative to peers regardless of minor scoring shifts.

Comparison studies by the National Institute for Educational Leadership show that this consistency boosts trust in grading across departments. Third, it supports mastery-based learning. Since the curve naturally clusters performance around central values while dampening extremes, it aligns well with competency-based education frameworks.

Teachers can more accurately identify true learning gaps, adjusting instruction to meet students where performance actually lies—not where distorted percentages might mislead. Finally, the Square Root Grading Curve enhances transparency. By anchoring grade allocation in observable statistical behavior, it reduces reliance on subjective interpretations of "behavioral credit" or arbitrary cutoffs, providing students and parents with clearer justification for grades.

Challenges and Considerations in Implementation

Despite its strengths, adopting the Square Root Grading Curve requires thoughtful implementation. Many educators accustomed to linear percentages may initially resist nonlinear scaling, perceiving it as obscure or unfair. Effective communication is essential: instructors and students must understand that grades reflect real performance, not abstract math.

Moreover, no single curve fits all. The transformation factor—here, the square root—should be calibrated to each institution’s academic culture, exam difficulty, and cohort makeup. Pilot testing with representative student groups helps fine-tune scaling parameters for optimal fairness.

Technical training is also critical. Teachers need tools to translate raw scores into curved grades efficiently, often through spreadsheets or learning management platforms built to apply the square root formula automatically. Integration with existing grading software can streamline this transition.

Lastly, while the Square Root Curve improves fairness, it does not eliminate human judgment. Faculty input remains vital to contextualize data, interpret performance beyond numerical patterns, and ensure grading honors both academic achievement and individual growth.

Expanding the Horizon: Broader Implications for Academic Assessment

The Square Root Grading Curve exemplifies how mathematical insight can reshape core educational practices.

Beyond improving fairness in course grading, its principles inspire innovation in other assessment domains—such as portfolio evaluation, formative feedback systems, and even standardized testing design. By grounding grading in empirical distributions, institutions foster greater equity, transparency, and trust. Embracing this approach signals a shift from arbitrary benchmarks to evidence-based calibration.

As education evolves toward personalized and competency-driven models, tools like the Square Root Grading Curve equip leaders to measure learning with greater precision and fairness. In an era where equity is paramount, mathematics becomes not a barrier but a bridge—connecting data to dignity, and grades to genuine achievement. The Square Root Grading Curve is more than a statistical trick; it is a testament to how disciplined thinking can enhance the heart of learning.

In a complex world, simplicity plus sophistication delivers win-win outcomes: students recognized fairly, institutions trusted, and education truly transformed.