The Delta Formula: How Small Differences Drive Major Mathematical Impact
The Delta Formula: How Small Differences Drive Major Mathematical Impact
Mathematics thrives not only on grand theorems but on the precise power of change—how infinitesimal shifts in input yield exact, measurable differences in output. At the heart of this dynamic lies the Delta Formula, a foundational principle quantifying the rate of change: Δy = f(Δx) / Δx, where a small change in the independent variable (Δx) determines the corresponding change in the dependent variable (Δy). This elegant trigonometric neighbor of calculus enables every engineer, economist, and scientist to model physical, financial, and social phenomena with unprecedented accuracy.
At its core, the Delta Formula embodies a simple yet profound relationship: small variations in input trigger predictable variations in output. Its practical application begins with careful observation—measuring how a 1% increase in pressure affects volume, or how a $0.01 change in interest rate alters loan repayment, all captured through finite differences. This quantification empowers decision-making under uncertainty, transforming qualitative assessments into objective, verifiable predictions.
Understanding the Delta Formula requires gratitude for its dual nature: theoretical elegance and empirical utility. Historically rooted in Newton’s and Leibniz’s breakthroughs in calculus, it now underpins modern numerical methods, optimization algorithms, and machine learning models. As Dr.
Lila Chen, applied mathematician at MIT, observes: “The true strength of the Delta Formula is not merely computing change—it’s enabling forward-looking insight.” This insight bridges abstract mathematics and tangible real-world outcomes, where even a rainfall increase of 2.5 mm/h can trigger measurable shifts in river discharge, crop yields, or urban flooding risk.
Mathematical Foundations: How Delta Expresses Variable Relationships
The Delta Formula, formally expressed as Δy ≈ f(Δx) / Δx for infinitesimal changes, approximates how dependent variables shift relative to input variations. In calculus, this expression converges to the derivative—slope of the tangent line representing instantaneous change—but remains vital in discrete settings.For example, consider a financial model where revenue R = p × q, with price p and quantity q. A 1% rise in price may increase revenue by 0.8% if demand elasticity is -0.8, captured precisely by ΔR/R ≈ Δp/p × Δq/q. Such finite differences form the backbone of sensitivity analysis—a technique used across industries to identify which parameters most influence system behavior.
In climate science, ΔT = α × ΔCO₂ quantifies warming sensitivity, where τ = 1/(C.sensitivity) gauges the climate’s lagged response. In data science, gradient descent—used to minimize loss




Related Post

<h2>The Torah in Islam: How Muslims Perceive the Sacred Script and Its Enduring Role</h2>

Club Pachuca: The Rising Force in Mexican and Global Football
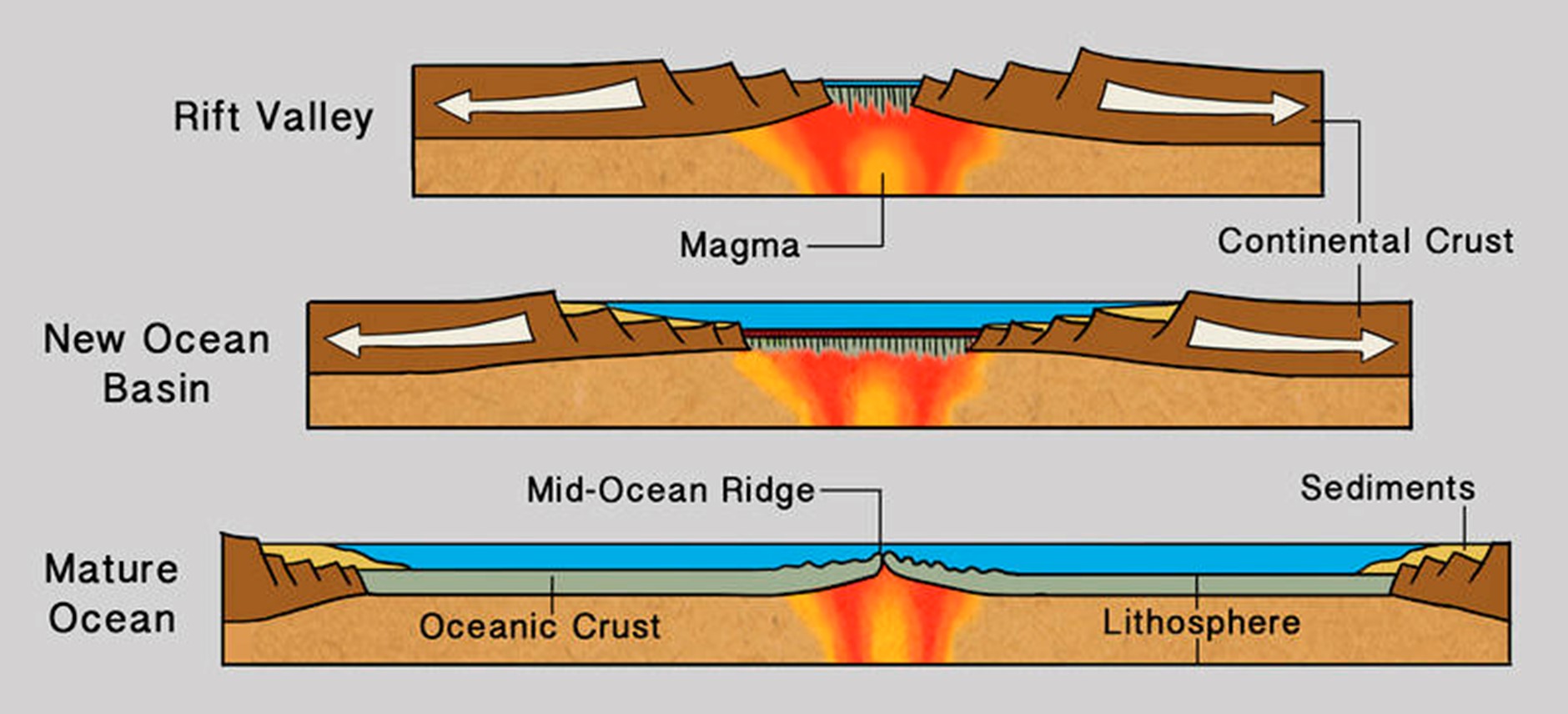
Underwater Rifts: How Ocean Ocean Divergent Boundaries Shape Earth’s Crust

