How To Calculate Atomic Mass: Mastering the Building Blocks of Matter

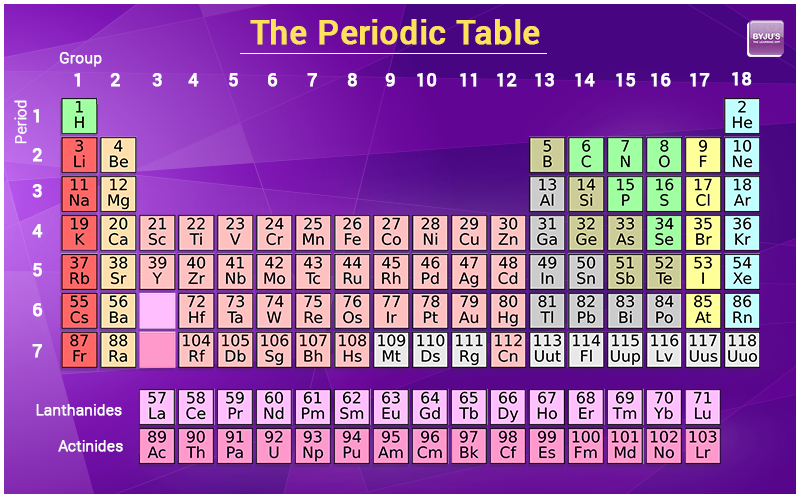
Understanding atomic mass is fundamental to chemistry, offering insights into the identity and behavior of elements. It represents the weighted average mass of an element’s naturally occurring isotopes, measured in atomic mass units (amu) or unified atomic mass units (u). Unlike an average of whole integers, atomic mass reflects the intricate distribution and abundance of isotopes, providing a precise quantitative measure essential for scientific calculations.

Calculating atomic mass requires a clear understanding of isotopes, their relative abundances, and their contributions to the element’s overall mass. Each isotope of an element carries a specific mass based on its proton and neutron count—typically listed on the periodic table, but rarely presented with context. The real power lies in combining these isotope masses with their natural abundances to derive a measurable value that defines the element’s identity.

This process transforms abstract atomic data into a concrete numberused by researchers, educators, and industry experts alike.

The Core Concept: What Is Atomic Mass?

Atomic mass is not simply the sum of protons and neutrons; it accounts for the weighted average of isotopes according to their natural occurrence percentages. This distinction separates the classical sum from the scientifically accurate average. While a single atom’s mass may vary slightly due to isotopic distribution, the atomic mass serves as a standardized reference—critical for stoichiometry, chemical equations, and material science.

Key Fact: Atomic mass values are expressed in atomic mass units (u), where 1 u equals 1/12th the mass of a carbon-12 atom. This standardization ensures consistency across scientific disciplines, enabling precise comparisons between elements and compounds.

Step-by-Step: Calculating Atomic Mass from Isotopic Data

To compute atomic mass, begin with accurate isotopic data: each isotope’s mass in atomic mass units and its natural abundance—usually expressed as a percentage or decimal fraction. For example, chlorine, with two primary isotopes, has: - Isotope Cl-35: mass ≈ 34.96885 u, abundance ≈ 75.77% or 0.7577 - Isotope Cl-37: mass ≈ 36.96590 u, abundance ≈ 24.23% or 0.2424 This distribution must reflect real-world natural ratios, not laboratory anomalies.

Only then can the weighted average be calculated using a precise formula. The calculation follows this method: 1. Convert abundance percentages into decimal form (e.g., 75.77% → 0.7577).

2. Multiply each isotope’s mass by its abundance fraction. 3.

Sum all weighted values to obtain the atomic mass. Using chlorine’s data: (34.96885 × 0.7577) + (36.96590 × 0.2424) = 26.49531 + 8.95817 = 35.45348 u Thus, chlorine’s atomic mass is approximately 35.45 u—a value that appears on the periodic table but carries the legacy of atomic structure and isotopic diversity behind it.

Real-World Examples and Diversification Across Elements

The process varies slightly between elements but follows the same logical framework.

Take oxygen, with three main isotopes: - O-16: mass 15.994915 u, abundance 99.76% (0.9976) - O-17: mass 16.999133 u, abundance 0.04% (0.0004) - O-18: mass 17.999160 u, abundance 0.20% (0.0020) Calculation: (15.994915 × 0.9976) + (16.999133 × 0.0004) + (17.999160 × 0.0020) = 15.9518 + 0.0068 + 0.035998 = 15.9946 u This mirrors chlorine’s method but highlights how elements differ in both isotopic abundance and precise atomic mass. These numbers underpin critical applications—from pharmaceuticals, where precise atomic mass ensures drug accuracy, to nuclear physics, where small mass differences influence reaction dynamics. Another illustrative case: uranium, dominant in energy production, features isotopes like O-238 (99.27% abundance, 238.05088 u) and O-235 (0.72%, 235.04391 u).

Its calculated atomic mass—around 238.03 u—directly informs reactor fuel design and safety thresholds.

Why Accuracy Matters: Applications Beyond the Equations

Accurate atomic mass values are not merely academic; they are vital to innovation and safety. In chemical manufacturing, precise atomic mass enables correct stoichiometric ratios, preventing waste and ensuring product purity.

In isotopic analysis, small measurement errors can distort scientific conclusions—whether tracking pollutants or studying metabolic pathways in medicine. Quantifying atomic mass accurately supports the development of advanced materials, fuels cleaner energy, and drives breakthroughs in nanotechnology. For educators, these values ground theoretical knowledge in measurable reality, helping students grasp the tangible link between atomic theory and the world they observe.

Experts emphasize, “The atomic mass is the cornerstone of quantitative science—without it, chemistry loses its predictive power.” By mastering its calculation, scientists and students alike unlock deeper understanding of matter’s fundamental architecture.

Final Insights: The Enduring Significance of Atomic Mass

The ability to calculate atomic mass transcends a classroom exercise; it is a gateway to interpreting the microscopic world with precision. From classroom labs to global energy systems, atomic mass serves as both a reference point and a dynamic indicator of isotopic behavior.

As research pushes into new frontiers—quantum computing, isotopic hydrology, and nuclear medicine—the clarity afforded by accurate atomic mass calculations becomes ever more critical. This singular number embodies the complexity of atomic structure in a single, powerful value—making the mathematics behind it indispensable to modern science and technology.